Droplet turbulence interaction
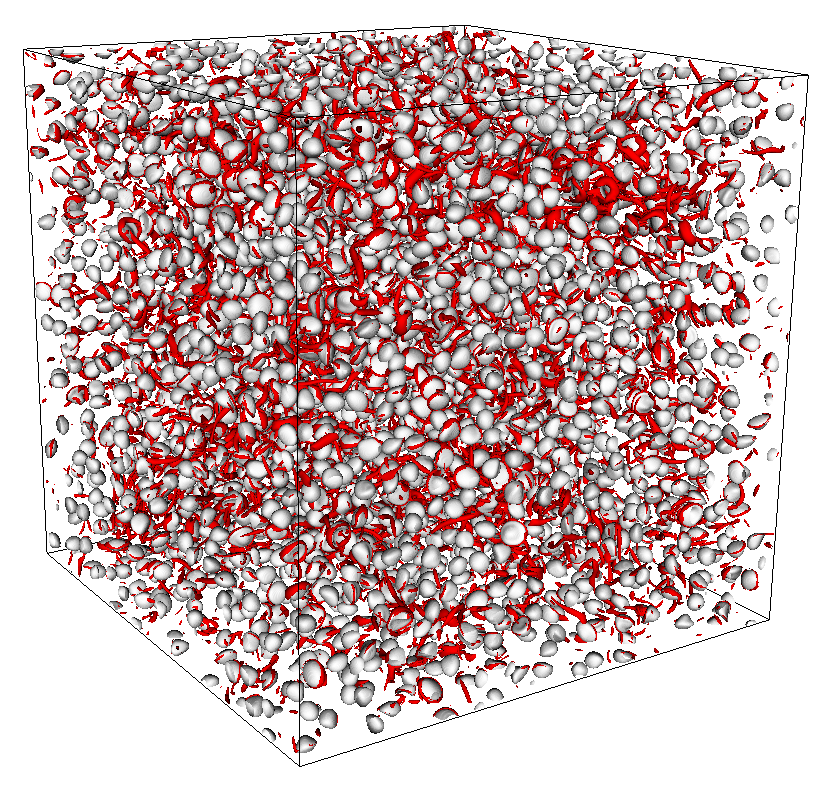
Interaction of liquid droplets with turbulence is important in numerous applications ranging from rain formation to oil spills to spray combustion. The physical mechanisms of droplet-turbulence interaction are largely unknown, especially when compared to that of solid particles. We have performed direct numerical simulations of droplets in decaying isotropic turbulence while resolving the flow inside and outside the droplets and accounting for surface tension. We have conducted a parametric study, varying one of three parameters: the density ratio between the droplet and the carrier fluid, the ratio of dynamic viscosities between the droplet and carrier fluid, and the surface tension coefficient. The turbulence kinetic energy budgets equations for droplet-laden decaying isotropic turbulence are derived for the first time. Additionally, we establish a relationship between the rate of work due to surface tension and the rate of change of the total droplet surface area. This link, coupled with the simulations, shows how droplet deformation, breakup, and coalescence influences the overall kinetic energy budget of droplet-laden turbulent flows. Such knowledge can be used to improve the predictive capabilities of computational models used in engineering design.
Reference: Dodd, M. S. & Ferrante, A. "On the interaction of Taylor length scale size droplets and isotropic turbulence." Journal of Fluid Mechanics, 806, 356-412, 2016PDF DOI
A fast pressure-correction method for two-fluid flows
A new pressure-correction method is developed for simulating incompressible two-fluid flows with large density and viscosity ratios. The method's main advantage is that the variable coefficient Poisson equation that arises in solving the incompressible Navier–Stokes equations for two-fluid flows is reduced to a constant coefficient equation, which can be solved using an FFT-based, fast Poisson solver. This reduction is achieved by splitting the variable-density pressure gradient in the governing equations. The validity of this splitting is demonstrated in numerical tests up to density and viscosity ratios of 10,000. Because the scheme can use a direct, FFT-based fast Poisson solver as opposed to an iterative method, the overall solution time of the Navier-Stokes equations is reduced by a factor of 10-40, and the resulting velocity field is divergence-free to machine epsilon.
Reference: Dodd, M. S. & Ferrante, A. "A fast pressure-correction method for incompressible two-fluid flows." Journal of Computational Physics, 273, 416-434, 2014PDF DOI
A mass-conserving volume-of-fluid method for droplet-laden turbulence
A mass-conserving volume-of-fluid (VoF) method is developed for application to droplet-laden isotropic turbulence. The method conserves mass locally and globally, and the volume fraction remains bounded. The volume fraction field is advanced in time using a geometric, split-advection method. Tests show that the method is second order accurate and twice as fast as comparable techniques. Application to droplet-laden decaying isotropic turbulence is demonstrated.
Reference: Baraldi, A., Dodd, M. S. & Ferrante, A. "A mass-conserving volume-of-fluid method: Volume tracking and droplet surface-tension in incompressible isotropic turbulence." Computers and Fluids, 96, 322-337, 2014PDF DOI
Particle dispersion in a turbulent boundary layer
Fundamental understanding of particle dispersion in turbulent flows can improve prediction of sedimentation processes and pollutant dispersion in the atmosphere. Practical turbulent flows are often statistically inhomogeneous and bounded by one or more walls. In this work, we have studied particle dispersion in a spatially developing turbulent boundary layer by performing direct numerical simulation. Fluid points and solid particles are released from a line source some distance from the wall and then tracked in a Lagrangian frame. The particle Stokes number is varied from 0.1 to 5. Dispersion statistics are found to be strongly influenced by particle inertia. As particle inertia increases, the particles' tendency to concentrate preferentially in the viscous sublayer increases. We also propose power laws for the long-time dispersion of the solid particles in the streamwise and wall-normal directions.
Reference: Dodd, M. S., Webster, K. & Ferrante, A. "Direct numerical simulation of particle dispersion in a spatially developing turbulent boundary layer." 7th International Conference on Computational Fluid Dynamics, Big Island, Hawaii, ICCFD7-2302, 2012